|













|
Al-Khwarizmi-the Father of
Algebra
Prof. Ibrahim B. Syed
President
Islamic Research Foundation
International, Inc.
Louisville, Kentucky
E-Mail:
President@irfi.org
Website:
WWW.IRFI.ORG
Every student who goes to
high school in every country in the world learns Algebra. The research
on brain development has shown that algebra concepts should begin as
early as Kindergarten. The National Council of Teachers of Mathematics
published new standards in 2000 that suggested students as young as
kindergarten should begin “algebraic reasoning.” The School at Columbia
University, a new private elementary school next to the Columbia campus,
second graders are beginning the second year of an experimental early
algebra program. The results of the first year show that after five
months of teaching basic algebra through patterns, second graders at The
School, and their counterparts at a similar lab school at the University
of Toronto, had a much better grasp of multiplication and algebraic
reasoning than students who began with a more advanced mathematical
base. The Columbia children were compared to a control group of second
graders at an elite Toronto private school. More and more early
algebraic reasoning is being thought of as very important to later
mathematical understanding, said Joan Moss, a researcher at the
Institute of Child Study at the University of Toronto, who initiated the
project. In
Germany, Japan, Argentina, Korea, France and other developed countries,
all students are expected to conquer beginning algebra. They start early
-- routinely in the sixth or seventh grade -- and study it thoroughly
until they reach high school.
"In the United States,
only about 25 percent of students in the middle grades get algebra.
Everywhere else, basically 100 percent get it at that point," said
William Schmidt, national coordinator of research for the Third
International Mathematics and Science Study. Widely known as TIMSS, the
study draws regular headlines because it usually shows American children
behind other children in the world. 1
In California, the
algebra overhaul is hitting two levels -- middle school and high school.
The state's academic standards now say that algebra should be taught
beginning in the eighth grade, a new and somewhat controversial ideal.
And state law now requires that all high school students, starting with
this year's freshmen, master Algebra 1 to graduate.
WHAT IS ALGEBRA?
Algebra
is a branch of mathematics that uses mathematical statements to describe
relationships between things that vary over time.
These
variables include things like the relationship between supply of an
object and its price. When we use a mathematical statement to describe a
relationship, we often use letters to represent the quantity that
varies, since it is not a fixed amount. These letters and symbols are
referred to as variables. The mathematical statements that
describe relationships are expressed using algebraic terms,
expressions, or equations (mathematical statements containing
letters or symbols to represent numbers). 2
Algebra is the study of
the properties of numbers and the study of the things that we can do
knowing those properties. Algebra is, or should be, a study in logic.
Algebra is the process of using logic to draw conclusions from things we
know to things that we do not know about until we apply algebraic
reasoning. 3
WHY LEARN ALGEBRA?
4
The question is why learn
Algebra? Careers today demand skills like problem solving, reasoning,
decision-making, and applying solid strategies etc. Algebra provides one
with a wonderful grounding in those skills - not to mention that it can
prepare one for a wide range of careers. Colleges require it and some
employers demand it. A required tool for many technical fields, Algebra
is a way to increase mathematical skills. Algebra is a great mental
workout and it's the only path to moving on to more advanced
mathematics. The Basics of Algebra consist of taking the real situation
and turn it into an equation. Secondly it makes us find out what the
unknown is. By applying Algebraic reasoning one can solve real-life
situations. Hence recently the SAT (Scholastic Aptitude Test) has
included questions on Algebra-II for high school students aspiring to go
to reputable and Ivy League Colleges.
One can argue
that one really does not "need" algebra unless one plans to teach it or
use it in a scientific profession. But before one puts away algebra
books, there are some good reasons "for" studying algebra.
Algebra is a very unique discipline. It is very abstract. The
abstract-ness of algebra causes the brain to think in totally new
patterns. That thinking process causes the brain to work, much like a
muscle. The more that muscle works out, the better it performs on OTHER
tasks. In simple terms, algebra builds a better brain (as do other
disciplines such as learning an instrument, doing puzzles, and, yes,
even some video games). When the brain is stimulated to think, the
hair-like dendrites of the brain grow more extensive and more complex
enabling more connections with other brain cells. We often hear that we
use only a small percentage of our brain's capacity. The study of
algebra is a way to increase our use of this marvelous muscle. By
studying algebra, more "highways" are "built" upon which future "cargo"
is transported -- cargo other than algebra.
One favorite
analogy is comparing the study of algebra to the construction of the
railway system in the United States in the 1800's. When railroads were
built, surely those men never conceived of the items that would be
transported on those rails more than a hundred years later. They could
not have imagined home appliances and computer equipment traveling over
that railway system. But they knew that building the transportation
system was important. So it is with the study of algebra – one learns
algebra by transporting numbers and variables -- later, those variables
will change and one will transport something useful for one's purposes.
An example is running an activities company in Hawaii. To run the
business one should do -- from creating forms, organizing activities for
up to 1100 people per week, with folks going off in multiple directions
for horseback riding, snorkeling, land tours, helicopter rides, deep sea
fishing, windsurfing, etc, etc, etc -- busses and vans were coming and
going at half hour intervals and only one person missed their ride --
out of 1100 people -- not too bad! So what's the point? The ability to
organize a rational procedure for handling this kind of chaos comes from
one’s algebra background. One should lay out the variables, design a
procedure, and follow the procedure. It is an intense form of
organization.
Which brings us to the right brain / left brain discussion. An actress,
actor, or artist of any kind is a "right brain" dominated person. These
people usually do not have an affinity for algebra. For the creative
mind, algebra is usually quite a struggle. Those making an attempt at
algebra bring themselves closer to understanding the mind of a "left
brain" person for whom math, science, and usually, languages come easy.
Much of our public school curriculum is based upon the latter -- a
"classical" education rather than an artistic "romantic" education.
There are other disciplines, which will help build a better brain, but
curriculum designers have chosen algebra as a universal "brain builder"
along with preparing those strong left-brain students for careers in
math and science.
Historically, algebra
is the study of solutions of one or several algebraic equations,
involving the polynomial (an expression of two or more terms) functions
of one or several variables. The case where all the polynomials have
degree one (systems of linear equations) leads to linear algebra. The
case of a single equation, in which one studies the roots of one
polynomial, leads to field theory and to the so-called Galois Theory.
The general case of several equations of high degree leads to algebraic
geometry, so named because the sets of solutions of such systems are
often studied by geometric methods. 5
Modern algebraists
have increasingly abstracted and axiomatized the structures and patterns
of argument encountered not only in the theory of equations, but in
mathematics generally. Examples of these structures include groups
(first witnessed in relation to symmetry properties of the roots of a
polynomial and now ubiquitous throughout mathematics), rings (of which
the integers, or whole numbers, constitute a basic example), and fields
(of which the rational, real, and complex numbers are examples). Some of
the concepts of modern algebra have found their way into elementary
mathematics education in the so-called new mathematics. 5
Some important
abstractions recently introduced in algebra are the notions of category
and functor, which grew out of so-called homological algebra. Arithmetic
and number theory, which are concerned with special properties of the
integers e.g., unique factorization, primes, equations with integer
coefficients (Diophantine equations), and congruences are also a part of
algebra. Analytic number theory, however, also applies the non algebraic
methods of analysis to such problems. 5
PRINCIPLES OF
MODERN ALGEBRA
Modern algebra is yet
a further generalization of arithmetic than is classical algebra. It
deals with operations that are not necessarily those of arithmetic and
that apply to elements that are not necessarily numbers. The elements
are members of a set and are classed as a group, a ring, or a field
according to the axioms that are satisfied under the particular
operations defined for the elements. Among the important concepts of
modern algebra are those of a matrix and of a vector space. 6
21st Century is
the age of Information Technology (IT) and modern computers that have
become ubiquitous and indispensable in everyday life, are the
foundations of IT.
Abu Ja'far Muhammad ibn Musa al-Khwarizmi,
(780 – 850 CE),
is the grandfather of computer science and the father of Algebra. He was
the popularizer of Arabic numerals, adopter of zero (the symbol, that
is) and the decimal system, astronomer, cartographer, in briefs an
encyclopedic scholar.
BAYT Al-HIKMA (House of Wisdom)
In the year 832,
Caliph Al Ma'mun [b. Baghdad, 786, d. Tarsus,
Cilicia, August 833] founded the "House of Wisdom" in Baghdad, a center
for study and research similar to the earlier Museum in Alexandria. Its
most famous scholars are the mathematicians Muhammad ibn Musa
Al-Khwarizmi and the
Banu Musa ("sons of Moses"), three brothers who directed the translation
of Greek works from Antiquity. 7
The modern word algorithm is derived from
his name, al-Khwarizmi, the best mathematician of his
age and thanks to his book, al-Kitab al-mukhtasar fi Hisab
al-jabr w'al-muqabala, (a book showing how to solve equations and
problems derived from ordinary life) which means "The Compendious Book
on Calculation by Completion and Balancing", was later mangled into
algebra, was the first written text on the subject. In
al-Khwarizmi's time, algebra was a practical system for solving all
kinds of problems "in cases of inheritance,
contracts, surveying, tax collection, legacies, partition,
lawsuits, and trade, and in all their dealings with one another, or
where the measuring of lands, the digging of canals, geometrical
computations, and other objects of various sorts and kinds are
concerned." Al-jabr was about removing the negative terms
from an equation, while al-muqabala meant "balancing" the
values of an equation across an equals sign.
It is the title of this text that gives us the word
"algebra". It is the first book to be written on algebra. In
al-Khwarizmi's own words, the purpose of the book is to teach:
What is easiest and most
useful in arithmetic, such as men constantly require in cases of
inheritance, legacies, partition, lawsuits, and trade, and in all their
dealings with one another, or where the measuring of lands, the digging
of canals, geometrical computations, and other objects of various sorts
and kinds are concerned.
This does not sound like the contents of an algebra
text, and indeed only the first part of the book is a discussion of what
we would today recognize as algebra. However it is important to realize
that the book was intended to be highly practical, and that algebra was
introduced to solve real life problems that were part of everyday life
in the Islamic empire at that time.
After introducing the natural numbers, he discusses
the solution of equations. His equations are linear or quadratic and are
composed of units (numbers), roots (x) and squares (x2). He
first reduces an equation to one of 6 standard forms, using the
operations of addition and subtraction, and then shows how to solve
these standard types of equations. He uses both algebraic methods of
solution and the geometric method of completing the square.
The next part of al-Khwarizmi's Algebra consists of
applications and worked examples. He then goes on to look at rules for
finding the area of figures such as the circle, and also finding the
volume of solids such as the sphere, cone, and pyramid. This section on
mensuration certainly has more in common with Hindu and Hebrew texts
than it does with any Greek work. The final part of the book deals with
the complicated Islamic rules for inheritance, but requires little from
the earlier algebra beyond solving linear equations. 8
TEXTBOOK OF ALGEBRA
9
Each chapter was followed by geometrical
demonstration and then many problems are worked out. Some of his
problems are formal while others were in practical context.
An example of his formal problem follows:
"If from a square I
subtract four of its roots and then take one-third of the remainder,
finding this equal to four of the roots, the square will be 256. "
He explained it in the
following manner:
"Since one-third of the
remainder is equal to four roots, one knows that the remainder itself
will equal 12 roots. Therefore, add this to the four, giving 16 roots.
This (16) is the root of the square. The above can also be stated in
terms of modern notation as 1/3 (x2 - 4x) = 4x."
Khwarizmi in a chapter on commercial transactions
states that "mercantile transactions and all things pertaining thereto
involve two ideas and four numbers." Karpinski in his translation of the
book explains:
The two ideas appear to be the notions of quantity
and cost; the four numbers represent unit of measure and price per unit,
quantity desired and cost of the same.
An example of
Al-Khwarizmi's mercantile problem: 9
"A man is hired to work
in a vineyard 30 days for 10 Dollars. He works six days. How much of the
agreed price should he receive?"
Explanation: "It is
evident that since days are one-fifth of the whole time; and it is also
evident that the man should receive pay having the same relation to the
agreed price that the time he works bears to the whole time, 30 days.
What we have proposed, is explained as follows. The month, i.e., 30
days, represents the measure, and ten represents the price. Six days
represents the quantity, and in asking what part of the agreed price is
due to the worker you ask the cost. Therefore multiply the price 10 by
the quantity 6, which is inversely proportional to it. Divide the
product 60 by the measure 30, giving 2 Dollars. This will be the cost,
and will represent the amount due to the worker."
The text book of Algebra
was intended to be highly practical and it was introduced to solve real
life problems that were part of everyday life in the Islamic world at
that time. Early in the book al- Khwarizmi wrote:-
"When I consider what
people generally want in calculating, I found that it always is a
number. I also observed that every number is composed of units, and that
any number may be divided into units. Moreover, I found that every
number which may be expressed from one to ten, surpasses the preceding
by one unit: afterwards the ten is doubled or tripled just as before the
units were: thus arise twenty, thirty, etc. until a hundred: then the
hundred is doubled and tripled in the same manner as the units and the
tens, up to a thousand; ... so forth to the utmost limit of numeration."10
SOLUTIONS OF EQUATIONS 11
Having introduced the natural numbers, al-Khwarizmi
introduces the main topic of this first section of his book, namely the
solution of equations. His equations are linear or quadratic and are
composed of units, roots and squares. For example, to al-Khwarizmi a
unit was a number, a root was x, and a square was x2.
However, although we shall use the now familiar algebraic notation in
this article to help the reader understand the notions, Al-Khwarizmi's
mathematics is done entirely in words with no symbols being used.
He first reduces an equation (linear or quadratic)
to one of six standard forms:
1. Squares equal to roots. Example: ax2
= bx
2. Squares equal to numbers. Example: ax2
= b
3. Roots equal to numbers. Example: ax = b
4. Squares and roots equal to numbers. Example: ax2
+ bx = c e.g. x2
+ 10 x = 39.
5. Squares and numbers equal to roots. Example: ax2
+ c = bx e.g. x2
+ 21 = 10 x.
6. Roots and numbers equal to squares. Example: ax2
= bx + c, e.g. 3 x + 4 =
x2.
The reduction is carried
out using the two operations of al-jabr and al-muqabala.
Here "al-jabr" means "completion" and is the process of removing
negative terms from an equation. For example, using one of al-Khwarizmi's
own examples, "al-jabr" transforms x2 = 40 x -
4 x2 into 5 x2 = 40 x. The
term "al-muqabala" means "balancing" and is the process of reducing
positive terms of the same power when they occur on both sides of an
equation. For example, two applications of "al-muqabala" reduces 50 + 3
x + x2 = 29 + 10 x to 21 + x2
= 7 x (one application to deal with the numbers and a second to
deal with the roots)
Al-Khwarizmi then shows
how to solve the six standard types of equations. He uses both algebraic
methods of solution and geometric methods. For example to solve the
equation x2 + 10 x = 39 he writes:-
... Square and 10
roots are equal to 39 units.
The question therefore in this type of equation is about as follows:
what is the square which combined with ten of its roots will give a sum
total of 39? The manner of solving this type of equation is to
take one-half of the roots just mentioned. Now the roots in the problem
before us are 10. Therefore take 5, which multiplied by
itself, gives 25, and an amount which you add to 39 giving
64. Having taken then the square root of this which is 8,
subtract from it half the roots, 5 leaving 3. The number
three therefore represents one root of this square, which itself, of
course is 9. Nine therefore gives the square.
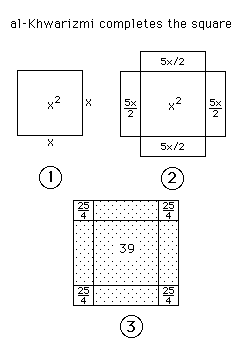
The geometric proof by
completing the square follows. Al-Khwarizmi starts with a square of side
x, which therefore represents x2 (Figure 1). To
the square we must add 10x and this is done by adding four
rectangles each of breadth 10/4 and length x to the square
(Figure 2). Figure 2 has area x2 + 10 x which
is equal to 39. We now complete the square by adding the four little
squares each of area. 5/2  5/2
= 25/4. 5/2
= 25/4.
Hence the outside square
in Fig 3 has area 4  25/4
+ 39 = 25 + 39 = 64. The side of the square is therefore 8. But the side
is of length 5/2 + x + 5/2 so x + 5 = 8, giving x =
3. 25/4
+ 39 = 25 + 39 = 64. The side of the square is therefore 8. But the side
is of length 5/2 + x + 5/2 so x + 5 = 8, giving x =
3.
Al-Khwarizmi continues his study of algebra in
Hisab al-jabr w'al-muqabala by examining how the laws of arithmetic
extend to arithmetic for his algebraic objects. For example he shows how
to multiply out expressions such as (a + b x) (c
+ d x)
although again we should emphasise that al-Khwarizmi
uses only words to describe his expressions, and no symbols are used.
Scientific historian, Roshdi Rashed 12 writes:-
Al-Khwarizmi's
concept of algebra can now be grasped with greater precision: it
concerns the theory of linear and quadratic equations with a single
unknown and the elementary arithmetic of relative binomials and
trinomials. ... The solution had to be general and calculable at the
same time and in a mathematical fashion, that is, geometrically founded.
... The restriction of degree, as well as that of the number of
unsophisticated terms, is instantly explained. From its true emergence,
algebra can be seen as a theory of equations solved by means of
radicals, and of algebraic calculations on related expressions...
If this interpretation
is correct, then al-Khwarizmi was as Sarton 12 writes:-
... the greatest
mathematician of the time, and if one takes all the circumstances into
account, one of the greatest of all time....
Al-Khwarizmi also wrote
a treatise on Hindu-Arabic numerals. The Arabic text is lost but a Latin
translation, Algoritmi de numero Indorum in English
Al-Khwarizmi on the Hindu Art of Reckoning gave rise to the word
algorithm deriving from his name in the title as mentioned earlier.
Unfortunately the Latin translation (translated into English) is
known to be much changed from al-Khwarizmi's original text (of which
even the title is unknown). The work describes the Hindu place-value
system of numerals based on 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0. The first
use of zero as a place holder in positional base notation was probably
due to al-Khwarizmi in this work. Methods for arithmetical calculation
are given, and a method to find square roots is known to have been in
the Arabic original although it is missing from the Latin version.
12
... the decimal place-value system was a fairly
recent arrival from India and ... al-Khwarizmi's work was the first to
expound it systematically. Thus, although elementary, it was of seminal
importance.
Khwarizmi developed
detailed trigonometric tables containing the sine functions which later
included tangent functions. Khwarizmi's book on arithmetic was
translated into Latin and published in Rome in 1857 by Prince Baldassare
Boncompagni and appears as part 1 of a volume entitled Tratti d'
aritmetica. The book is titled as Algorithmi de numero indorum
which means "Khwarizmi concerning the Hindu art of reckoning." Many of
his books were translated into Latin and used as a principle
mathematical text book in European universities until sixteenth century.
Among them these two books had important place: Kitab al-Jama
wal-Tafreeq bil Hisab al-Hindi and Kitab al-Jabr wa
al-muqabala.
Khwarizmi's contribution
and influence are tremendous. Two important books on arithmetic,
Carmen de Algorismo and Algorismus vulgaris which were
written in twelfth and thirteenth century respectively owe a lot to the
Khwarizmi's book and were used for several hundred years in Europe. Abu
Kamil whose work on mathematics was based on Khwarizmi's works kept the
influence of Khwarizmi on Leonardo of Pisa, a thirteenth century scholar
and up to Middle Ages and during the Renaissance. 9
ASTRONOMY 13
He also wrote an important work on astronomy, covering calendars,
calculating true positions of the sun, moon and planets, tables of sines
and tangents, spherical astronomy, astrological tables, parallax and
eclipse calculations, and visibility of the moon. Although his
astronomical work is based on that of the Indians, and most of the
values from which he constructed his tables came from Hindu astronomers,
al-Khwarizmi must have been influenced by Ptolemy's work too.
Al-Khwarizmi performed detailed calculations of the positions of the
Sun, Moon, and planets, and did a number of eclipse calculations. In
addition to an important treatise on Astronomy, Al-Khwarizmi wrote a
book on astronomical tables, which were also translated into European
languages and, later, into Chinese.
GEOGRAPHY 14
In geography, he wrote the book called Kitab
Surat al- ard (book of the form of the earth). His works differed
from Ptolemy's and he corrected Ptolemy's views in detail. It is a
description of a world (known world at that time) map and contains a
list of the coordinates of the important places on it. He corrected the
distortion that Ptolemy's map had with regard to the length of the
Mediterranean. It was much more accurate. However, it failed to replace
the Ptolemaic geography used in Europe. He wrote many other books on
topics such as clocks, sundials and astrolabes.
Al-Khwarizmi wrote a
major work on geography which gives latitudes and longitudes for 2,402
cities and landmarks, forming the basis for a world map. The book, which
is based on Ptolemy's Geography, lists with latitudes and longitudes,
cities, mountains, seas, islands, geographical regions, and rivers. The
manuscript includes maps which on the whole are more accurate than those
of Ptolemy.
A number of minor works were written by
al-Khwarizmi on topics such as the astrolabe, on which he wrote two
works, on the sundial, and on the Jewish calendar. He also wrote a
political history containing horoscopes of prominent persons.
Al-Khwarizmi systematized and corrected Ptolemy’s research in geography
and astronomy/astrology, using his own original findings. He supervised
the work of 70 geographers to create a map of the then "known world".
Amazingly this map of the "known world" shows the pacific coast of South
America-about 700 years before Columbus discovered America.
He is also reported to
have collaborated in the degree measurements ordered by Khalifah
(Caliph) Mamun al-Rashid were aimed at measuring of volume and
circumference of the earth. His geography book entitled "Kitab
Surat-al-Ard," including maps, was also translated. His other
contributions include original work related to clocks, sundials and
astrolabes. He also wrote Kitab al-Tarikh and Kitab al-Rukhmat (on
sundials).
IMPACT ON EUROPE
In 1140 Robert of Chester (who read mathematics in Spain) translated the
Arabic title into Latin as Liber algebrae et almucabala, then
ultimately gave its name to the discipline of algebra. The Spanish Jew,
John of Seville, produced another Latin version
When his work became known in Europe through Latin translations, his
influence made an indelible mark on the development of science in the
West: his algebra book introduced that discipline to Europe
"unknown till then” and
became the standard mathematical text at European universities until the
16th century.
In the 16th century it is found in English as algiebar and almachabel
and in various other forms but was finally shortened to algebra.
He is one of the Muslim scholars who laid the foundations for Europe’s
Renaissance and the Scientific Revolution.
He also wrote on mechanical devices like the clock, astrolabe, and
sundial. His other contributions include tables of trigonometric
functions, refinements in the geometric representation of conic
sections, and aspects of the calculus of two
errors.
15
CONCEPT OF COLLEGE
16
The idea of the college was a concept which was
borrowed from Muslims. The first colleges appeared in the Muslim world
in the late 600's and early 700's. In Europe, some of the earliest
colleges are those under the University of Paris and Oxford they were
founded around the thirteenth century. These early European colleges
were also funded by trusts similar to the Islamic ones and legal
historians have traced them back to the Islamic system. The internal
organization of these European colleges was strikingly similar to the
Islamic ones, for example the idea of Graduate (Sahib) and undergraduate
(mutafaqqih) is derived directly from Islamic terms.
Several of Al-Khwarizmi's books were translated into Latin in the early
l2 th century by Adelard of Bath and Gerard of Cremona. The treatises on
Arithmetic, Kitab al-Jam'a wal-Tafreeq bil Hisab al-Hindi, and the one
on Algebra, Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah, are known only
from Latin translations.
Introduction of Arabic numerals provided a pivotal advance over the
cumbersome Roman numerals. This development of a more convenient number
system assisted progress in science, accounting and bookkeeping. Key to
this was the use of the number zero, a concept unknown to the West. The
use of this number system (Arabic numerals) spread throughout the Muslim
world over the next two centuries, assisting the development of science.
The Arabic numeral system was first mentioned in Europe around 1200 CE,
but Christian adherence to the Roman system hindered its use and
introduction. It was only fully accepted in Europe after it was adopted
by the Italian traders in the Renaissance of the 16th century, who
followed the practice of their Arab trading partners.
17
MUSLIM IMPACT ON EUROPE 18
During the Middle Ages the Islamic World had a very
significant impact upon Europe, which in turn cleared the way for the
Renaissance and the Scientific Revolution. In the Medieval age, Islam
and Muslims influenced Europe in a number of different ways. One of the
most important of these subjects was Science.
Ever since Islam was born, Muslims had made immense
leaps forward in the area of Science. Cities like Baghdad, Damascus,
Cairo and Cordoba were the centers of civilization. These cities were
flourishing and Muslim scientists made tremendous progress in applied as
well as theoretical Science and Technology. In Europe, however, the
situation was much different. Europe was in the Dark Ages. It had no
infrastructure or central government. To the Muslims, Europe was
backward, unorganized, carried no strategic importance and was
essentially irrelevant. This considering the time period was in fact
true. Nevertheless the Catholic Church (which at the time was the
strongest institution in Europe) successfully convinced Christian Europe
that the Muslims were infidels. This caused Europeans to think that
Muslims were culturally inferior to Europe and thus Europe was unable to
benefit from the new scientific discoveries being made in the Islamic
lands before the 1100’s. By doing this Europe kept itself in the Dark
Ages while from China to Spain Islamic Civilization prospered. During
the Crusades there was limited contact between Muslims and Christians
and not much was transferred. As A. Lewis explains, "The Crusaders were
men of action, not men of learning". The real exchange of ideas which
led to the Scientific revolution and to the renaissance occurred in
Muslim Spain.
Cordoba was the capital of Muslim Spain. It soon
became the center for intellectual enlightenment and learning for the
entire Europe. Scholars and students from various parts of the world and
Europe came to Cordoba to study. The contrast in intellectual activity
is demonstrated best by one example: ‘In the ninth century, the library
of the monastery of St. Gall was the largest in Europe. It boasted 36
volumes. At the same time, that of Cordoba contained over 500,000.
Arabic
Mathematics Worldwide 19
In the 11th century, the Arab
mathematical foundation was one of the strongest in the world. The
Muslim mathematicians had invented geometrical algebra and had taken it
to advanced levels, capable of solving third and fourth degree
equations. The world witnessed a new stage in the development of
mathematical science, driven by the numerous translated works from
Arabic into European languages.
Unquestionably, Al-Khwarizmi was very influential
with his methods on arithmetic and algebra which were translated into
much of southern Europe. Again, these translations became popular as
algorismi – a term which is derived from the name of Al-Khwarizmi.
Not all went smoothly nonetheless. The Arabic numerals introduced by Al-Khwarizmi,
like much of new mathematics, were not welcomed wholeheartedly. In fact,
in 1299 there was a law in the commercial center of Florence (Italy)
forbidding the use of such numerals. Initially, only universities dared
use them, but later they became popular with merchants, and eventually
became commonly used.
In time, Europe realized the great potential value
of the Arab mathematical contributions and put into popular use all that
seemed practical. The sciences, with mathematics as their essence,
flourished and developed into the disciplines we know today. None would
have been the same though, had it not been for that book on restoration,
or had the zero not been invented, or had the Arabic numerals not made
their way to Europe. That “fondness of science,” which inspired an early
Arab mathematician to propose calculating by al-jabr and al-muqabala,
did much to make the world run as we know it today.
NUMBER ZERO 20
The 10th
millennium saw Muslim mathematical study concentrated in three main
sub-disciplines. These were the ongoing progress in algebra, the
development of arithmetic algorithms, and the increasing complexity in
geometry. In addition, the introduction of the zero was destined to
revolutionize mathematics as it allowed for key innovations. It was
proposed by Muhammad Bin Ahmad in 967 CE.
Zero arrived in the West much later, in 13th
century.
In the field of Mathematics the number Zero (0) and the decimal system
was introduced to Europe, which became the basis for the Scientific
revolution. The Arabic numerals were also transferred to Europe, this
made mathematical tasks much easier, problems that took days to solve
could now be solved in minutes. The works of Al-Khwarizmi (his Latin
name was Alghorismus) were translated into Latin. Al-Khwarizmi
(Alghorismus), from whom the mathematical term algorism was derived,
wrote Sindh Ind, a compilation of astronomical tables. He, more
importantly, laid the ground work for algebra and found methods to deal
with complex mathematical problems, such as square roots and complex
fractions. He conducted numerous experiments, measured the height of the
earth's atmosphere and discovered the principle of the magnifying lens.
Many of his books were translated into European languages. Trigonometric
work by Alkirmani of Toledo was translated into Latin (from which we get
the sine and cosine functions) along with the Greek knowledge of
Geometry by Euclid. Along with mathematics, masses of other knowledge in
the field of physical science was transferred. 21
Famous
works
22
Al-Jabr
wa-al-Muqabilah from
whose title came the name "Algebra"
Kitab al-Jam'a
wal-Tafreeq bil Hisab al-Hindi
(on Arithmetic, which survived in a Latin translation but was lost in
the original Arabic)
Kitab
Surat-al-Ard (on
geography)
Istikhraj Tarikh
al-Yahud (about the
Jewish calendar)
Kitab al-Tarikh
Kitab al-Rukhmat
(about sun-dials)
East to Europe
23
The agents of globalization are neither European
nor exclusively Western, nor are they necessarily linked to Western
dominance. Indeed, Europe would have been a lot poorer - economically,
culturally and scientifically - had it resisted the globalization of
mathematics, science and technology at that time.
And today, the same principle applies, though in
the reverse direction (from West to East). To reject the globalization
of science and technology because it represents Western influence and
imperialism would not only amount to overlooking global contributions -
drawn from many different parts of the world - that lie solidly behind
so-called Western science and technology, but would also be quite a daft
practical decision, given the extent to which the whole world can
benefit from the process.
Breaking boundaries
23
Certainly, the Renaissance, the Enlightenment and
the Industrial Revolution were great achievements - and they occurred
mainly in Europe and, later, in America. Yet many of these developments
drew on the experience of the rest of the world, rather than being
confined within the boundaries of a discrete Western civilization.
Our global civilization is a world heritage - not
just a collection of disparate local cultures. When a modern
mathematician in Boston invokes an algorithm to solve a difficult
computational problem, he/she may not be aware that he/she is helping to
commemorate the Arab mathematician Mohammad Ibn Musa-al-Khwarizmi, who
flourished in the first half of the ninth century. (The word algorithm
is derived from the name al-Khwarizmi.)
The square root of math itself
23
There is a chain of
intellectual relations that link Western mathematics and science to a
collection of distinctly non-Western practitioners, of whom al-Khwarizmi
was one. (The term algebra is derived from the title of his famous book
Al-Jabr wa-al-Muqabilah.)
Indeed, al-Khwarizmi
is one of many non-Western contributors whose works influenced the
European Renaissance and, later, the Enlightenment and the Industrial
Revolution. The West must get full credit for the remarkable
achievements that occurred in Europe and Europeanized America, but the
idea of an immaculate Western conception is an imaginative fantasy.
Modern prosperity, with
all its improvement in welfare, has been delivered to humanity by
science and technology. In the last two centuries especially, science
has delivered better lives for people, longer lives, and for larger
populations. The key to unlocking the source of these benefits was
scientific method, the relentless search for truth through observation,
theorizing and experimentation.
In the 13th century the Muslim world,
with its development of the culture of philosophy, science, mathematics,
astronomy, physics, chemistry and medicine, led the world. The Muslim
world once possessed in its hands the keys to the future prosperity that
technology could deliver. Not only that, but with the invention of
double entry bookkeeping, it possessed in its hands the blueprint of the
plans for the modern corporation.
Eventually, after several hundred years, Europe was able to absorb this
knowledge and overthrow the dark constraint of its own religion to
unlock the mysteries of science and discover the path to prosperity. If
the Muslim world had been able to continue on the Qur'anic commands on
scientific research, the cause of human progress would have been
advanced by about five hundred years. 17
CONCLUSION
In conclusion algebra and algorithms are enabling the building of
computers, and the creation of encryption. The modern technology
industry would not exist without the contributions of Muslim
mathematicians like Al-Khwarizmi.
Ms. Carly Fiorina, Hewlett-Packard's Chairman and CEO delivered a speech
in Minneapolis, Minnesota on September 26, 2001. The title of her speech
was 'TECHNOLOGY, BUSINESS AND OUR WAY OF LIFE: WHAT'S NEXT". 24
She said "There was once a civilization that was the greatest in the
world." ……."And this civilization was driven more than anything, by
invention. Its architects designed buildings that defied gravity. Its
mathematicians created the algebra and algorithms that would enable the
building of computers, and the creation of encryption. Its doctors
examined the human body, and found new cures for disease. Its
astronomers looked into the heavens, named the stars, and paved the way
for space travel and exploration." "When other nations were afraid of
ideas, this civilization thrived on them, and kept them alive. When
censors threatened to wipe out knowledge from past civilizations, this
civilization kept the knowledge alive, and passed it on others."
"While modern Western civilization shares many of these traits, the
civilization I'm talking about was the Islamic world from the year 800
to 1600, which included the Ottoman Empire and the courts of Baghdad,
Damascus and Cairo, and enlightened rulers like Suleiman the
Magnificent."
"Although we are often unaware of our indebtedness to this other
civilization, its gifts are very much part of our heritage. The
technology industry would not exist without the contributions of Arab
mathematicians. Sufi poet-philosophers like Rumi challenged our notions
of self and truth. Leaders like Suleiman contributed to our notions of
tolerance and civic leadership. And perhaps we can learn a lesson from
his example: It was leadership based on meritocracy, not inheritance.
It was leadership that harnessed the full capabilities of a very diverse
population-that included Christianity, Islamic and Jewish traditions."
REFERENCES
2.
cstl.syr.edu/fipse/Algebra/Unit1/algebra.htm
9. http://members.tripod.com/~khorasan/TajikPersonalities/Khwarizmi.htm
10. http://www.yorku.ca/sasit/sts/sts3700b/lecture02a.html
11. http://www-gap.dcs.st-and.ac.uk/~history/Mathematicians/Al-Khwarizmi.html
12. R Rashed, The
development of Arabic mathematics: between arithmetic and algebra
(London, 1994). www-groups.dcs.st-and.ac.uk/ ~history/Mathematicians/Al-Khwarizmi.html
14. http://www.stetson.edu/~efriedma/periodictable/html/Am.html
15. http://www.ummah.com/forum/archive/index.php/t-4425.html
16. How Islam Influenced Science, by Macksood Aftab, Managing Editor,
The Islamic Herald, March 1995.
http://www.themodernreligion.com/science/science_influence.htm
17. IB Syed.: Rise and Fall of Muslims. http://www.irfi.org
18. www.ais.org/~bsb/Herald/Previous/95/science.html
19.
O’Connor, J. J. and E. F. Robertson. “Arab mathematics: forgotten
brilliance.”
The Mac Tutor History of Mathematics Archive. John J. O’Connor and
Edmund F. Robertson. 2001. School of Mathematics and Statistics at
University of St. Andrews, Scotland. 2001. <http://www-groups.dcs.st-andrews.ac.uk/'.history/
/HistTopics/Arabic_mathematics.html>
20. http://www.alshindagah.com/sepoct2002/arab.html
21. How Islam Influenced Science,
by Macksood Aftab,
Managing Editor
The Islamic Herald,
March 1995.
http://www.geocities.com/WestHollywood/Park/6443/Science/science_influence.htm
22. http://www.answers.com/topic/al-khwarizmi
23.
Does Globalization Equal Westernization?
By
Amartya Sen. The Globalist,
Monday, March 25, 2002 http://www.theglobalist.com/DBWeb/StoryId.aspx?StoryId=2353
24.
CARLY FIORINA, MINNEAPOLIS, MINNESOTA , SEPTEMBER 26, 2001
"TECHNOLOGY, BUSINESS AND OUR WAY OF LIFE: WHAT'S NEXT" http://www.hp.com/hpinfo/execteam/speeches/fiorina/minnesota01.html
|
